R*O-система
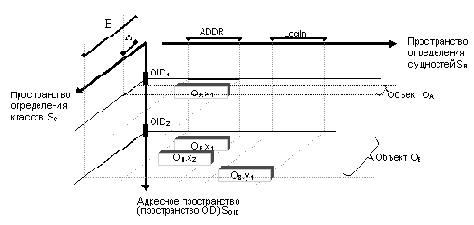
Рис. 4. R*O-система
Проекция этой системы (которая в силу отрогональности R- и O-компонентов автор называет R*O - системой) на плоскость (SC-SOID) дает следующую картину (рис.5)
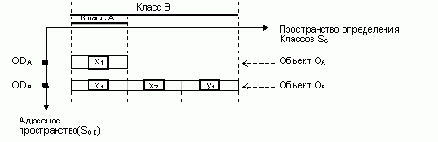
Рис. 5. O-проекция R*O-системы
(Еще раз необходимо повторить, что пространство определения объектных типов является сложным и многомерным. Однако в любом случае оно может рассматриваться как проекция пространства с большим числом измерений )
Видно что данная проекция является О - системой, где каждый ее элемент (т.е. один из кортежей содержащих информацию об объекте) может быть идентифицирован выражением вида { ( адрес объекта в системе).(положение элемента в схеме (т.е. в классе) описывающей данный объект) }. Поэтому для однозначного определения элементов для каждого из них должна поддерживаться следующая информация.
Именно эта информация является существенной для того чтобы кортеж мог рассматриваться как осмысленная часть идентифицируемого объекта.
Проекция R*O-системы на плоскость (SR-SOID) будет выглядеть следующим образом (рис.6)

Рис. 6. R-проекция R*O-системы
Пунктирные стрелки показывают что:
Далее будет показано, что эта информация также может быть описана в терминах реляционной модели.
Таким образом реляционная и объектная системы могут быть рассмотрены как ортогональные проекции общей R*O-системы. Можно предположить, что свойства R*O-системы определяются произведением свойств ее проекций. Объект существующий в этой системе является идентифицируемым и осмысленным набором кортежей. Отношение является доменом атрибута скалярного(базового) типа.
